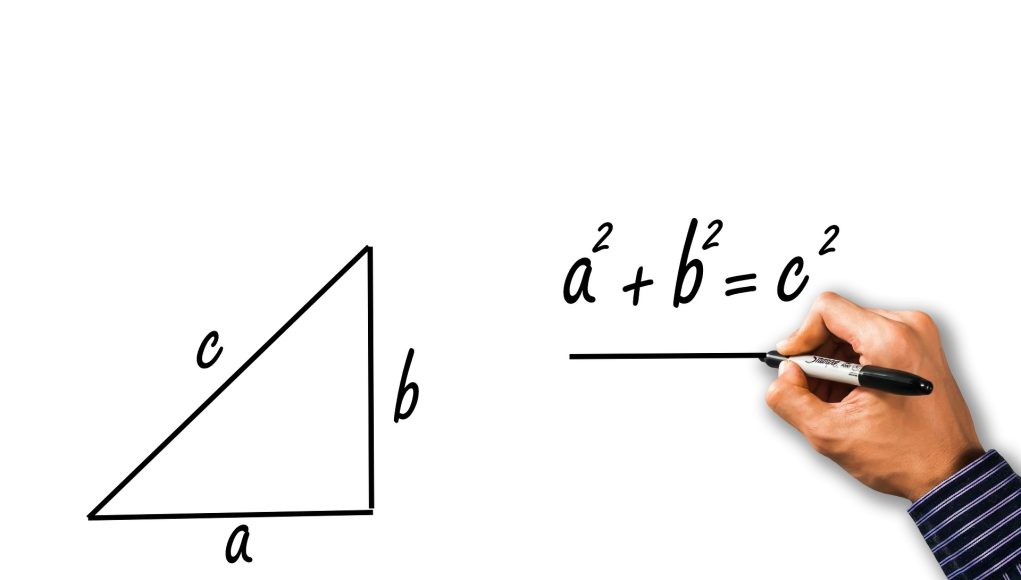Calculer un aire d’un triangle est une compétence mathématique fondamentale. Cela est essentiel que ce soit pour résoudre des problèmes géométriques, pour des applications dans la construction ou l’architecture.
Dans cet article, nous explorerons différentes méthodes et formules pour calculer l’aire d’un triangle, que vous pourrez appliquer dans diverses situations.
Triangle équilatéral
Un triangle équilatéral a trois côtés de même longueur et trois angles égaux de 60 degrés. Pour calculer l’aire d’un triangle équilatéral, vous pouvez utiliser la formule suivante :
Aire = (côté^2 x √3) / 4
où « côté » est la longueur d’un côté du triangle équilatéral. Il s’agit de la méthode la plus simple pour calculer l’aire de ce type de triangle.
Triangle rectangle
Un triangle rectangle a un angle de 90 degrés. Vous pouvez utiliser le théorème de Pythagore pour calculer son aire. Si « a » et « b » sont les longueurs des deux côtés perpendiculaires et « c » est l’hypoténuse, la formule est la suivante :
Aire = (a x b) / 2
Il s’agit d’une méthode simple pour calculer l’aire d’un triangle rectangle.
Triangle quelconque
Pour un triangle quelconque, vous pouvez utiliser la formule de l’aire de Héron. Si vous connaissez les longueurs de tous les côtés (a, b, et c) et que « s » est le semi-périmètre (la moitié du périmètre), la formule est la suivante :
Aire = √(s x (s – a) x (s – b) x (s – c))
où
s = (a + b + c) / 2
Pour utiliser cette formule, vous devez d’abord calculer le semi-périmètre à l’aide des longueurs des côtés. Ensuite, vous pouvez calculer l’aire.
Calcul à l’aide de la base et de la hauteur
Une méthode courante pour calculer l’aire d’un triangle est d’utiliser la base et la hauteur. Si vous connaissez la longueur de la base (b) et la hauteur (h) perpendiculaire à la base, vous pouvez utiliser la formule suivante :
Aire = (base x hauteur) / 2
Il s’agit d’une méthode simple qui est souvent utilisée lorsque les dimensions du triangle sont bien connues.
L’aire d’un triangle à l’aide de la règle du demi-produit des côtés
Une autre méthode pour calculer l’aire d’un triangle utilise la règle du demi-produit des côtés. Si vous connaissez les longueurs de deux côtés (a et b) et l’angle θ entre eux, vous pouvez utiliser la formule suivante :
Aire = (1/2) x a x b x sin(θ)
Cette formule est utile lorsque vous avez des informations sur deux côtés et l’angle entre eux.
L’aire d’un triangle à l’aide de vecteurs
En utilisant des vecteurs, vous pouvez également calculer l’aire d’un triangle. Dans le cas où vous avez les coordonnées de trois points du triangle (A(x1, y1), B(x2, y2), et C(x3, y3)), la formule est la suivante :
Aire = (1/2) x |(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2))|
Cette méthode est utile lorsque vous travaillez avec des coordonnées cartésiennes.
L’aire d’un triangle à l’aide de la matrice de déterminant
Une autre méthode avancée utilise la matrice de déterminant. Dans le cas où vous avez les coordonnées des sommets du triangle (A(x1, y1), B(x2, y2), et C(x3, y3)), la formule est la suivante :
Aire = (1/2) x |det([x1, x2, x3], [y1, y2, y3], [1, 1, 1])|
Il s’agit d’une méthode plus complexe, mais elle peut être utile dans des contextes mathématiques avancés.
Le calcul de l’aire d’un triangle peut être accompli de plusieurs manières en fonction des informations dont vous disposez. En comprenant ces différentes méthodes, vous serez en mesure de résoudre des problèmes de géométrie. De plus, il est important d’appliquer ces compétences dans divers domaines d’application.